Skip to contents

Predict method for Bayesian VARs

Source: R/utility_functions.R
predict.bayesianVARs_bvar.Rd

Simulates from (out-of-sample) predictive density for Bayesian VARs estimated via bvar() and computes log predictive likelhoods if ex-post observed data is supplied.

Usage

# S3 method for class 'bayesianVARs_bvar'
predict(
  object,
  ahead = 1L,
  each = 1L,
  stable = TRUE,
  simulate_predictive = TRUE,
  LPL = FALSE,
  Y_obs = NA,
  LPL_VoI = NA,
  ...
)

Arguments

object

A bayesianVARs_bvar object, obtained from bvar().

ahead

Integer vector (or coercible to such), indicating the number of steps ahead at which to predict.

each

Single integer (or coercible to such) indicating how often should be drawn from the posterior predictive distribution for each draw that has been stored during MCMC sampling.

stable

logical indicating whether to consider only those draws from the posterior that fulfill the 'stable' criterion. Default is TRUE.

simulate_predictive

logical, indicating whether the posterior predictive distribution should be simulated.

LPL

logical indicating whether ahead-step-ahead log predictive likelihoods should be computed. If LPL=TRUE, Y_obs has to be specified.

Y_obs

Data matrix of observed values for computation of log predictive likelihood. Each of ncol(object$Yraw) columns is assumed to contain a single time-series of length length(ahead).

LPL_VoI

either integer vector or character vector of column-names indicating for which subgroup of time-series in object$Yraw a joint log predictive likelihood shall be computed.

...

Currently ignored!

Value

Object of class bayesianVARs_predict, a list that may contain the following elements:

  • predictions array of dimensions c(length(ahead), ncol(object$Yraw), each * dim(object$PHI)[3]) containing the simulations from the predictive density (if simulate_predictive=TRUE).

  • LPL vector of length length(ahead) containing the log-predictive-likelihoods (taking into account the joint distribution of all variables) (if LPL=TRUE).

  • LPL_univariate matrix of dimension c(length(ahead), ncol(object$Yraw) containing the marginalized univariate log-predictive-likelihoods of each series (if LPL=TRUE).

  • LPL_VoI vector of length length(ahead) containing the log-predictive-likelihoods for a subset of variables (if LPL=TRUE and LPL_VoI != NA).

  • Yraw matrix containing the data used for the estimation of the VAR.

  • LPL_draws matrix containing the simulations of the log-predictive-likelihood (if LPL=TRUE).

  • PL_univariate_draws array containing the simulations of the univariate predictive-likelihoods (if LPL=TRUE).

  • LPL_sub_draws matrix containing the simulations of the log-predictive-likelihood for a subset of variables (if LPL=TRUE and LPL_VoI != NA).

See also

stable_bvar(), plot.bayesianVARs_predict(), pairs.bayesianVARs_predict().

Examples

# Access a subset of the usmacro_growth dataset
data <- usmacro_growth[,c("GDPC1", "CPIAUCSL", "FEDFUNDS")]

# Split data in train and test
train <- data[1:(nrow(data)-4),]
test <- data[-c(1:(nrow(data)-4)),]

# Estimate model using train data only
mod <- bvar(train, quiet = TRUE)

# Simulate from 1-step to 4-steps ahead posterior predictive and compute
# log-predictive-likelihoods
predictions <- predict(mod, ahead = 1:4, LPL = TRUE, Y_obs = test)
#> 'stable=TRUE': Calling 'stable_bvar()' to discard those posterior
#>           draws that do not fulfill the stable criterion.
#> 
#> 490/1000 stable posterior draws remaining for prediction!

# Summary
summary(predictions)
#> 
#> LPL:
#>   t+1   t+2   t+3   t+4 
#> 3.295 8.963 8.848 6.618 
#> 
#> Marginal univariate LPLs:
#>      GDPC1 CPIAUCSL FEDFUNDS
#> t+1 -1.208   0.4945    3.705
#> t+2  2.811   2.7032    3.380
#> t+3  2.986   2.5687    3.225
#> t+4  3.086   0.4691    3.077
#> 
#> Prediction quantiles:
#> , , GDPC1
#> 
#>          t+1        t+2       t+3       t+4
#> 5%  -0.06271 -0.0358741 -0.025896 -0.021977
#> 50% -0.01847  0.0003222  0.007422  0.007056
#> 95%  0.03786  0.0396699  0.042156  0.041783
#> 
#> , , CPIAUCSL
#> 
#>           t+1       t+2       t+3       t+4
#> 5%  -0.018501 -0.018386 -0.016577 -0.013903
#> 50% -0.008211 -0.005274 -0.002744 -0.001245
#> 95%  0.003095  0.006904  0.010319  0.010655
#> 
#> , , FEDFUNDS
#> 
#>           t+1       t+2       t+3       t+4
#> 5%  -0.017187 -0.029766 -0.035690 -0.046158
#> 50% -0.002658 -0.003953 -0.004949 -0.005525
#> 95%  0.014293  0.020864  0.026225  0.028602
#> 

# Visualize via fan-charts
plot(predictions)


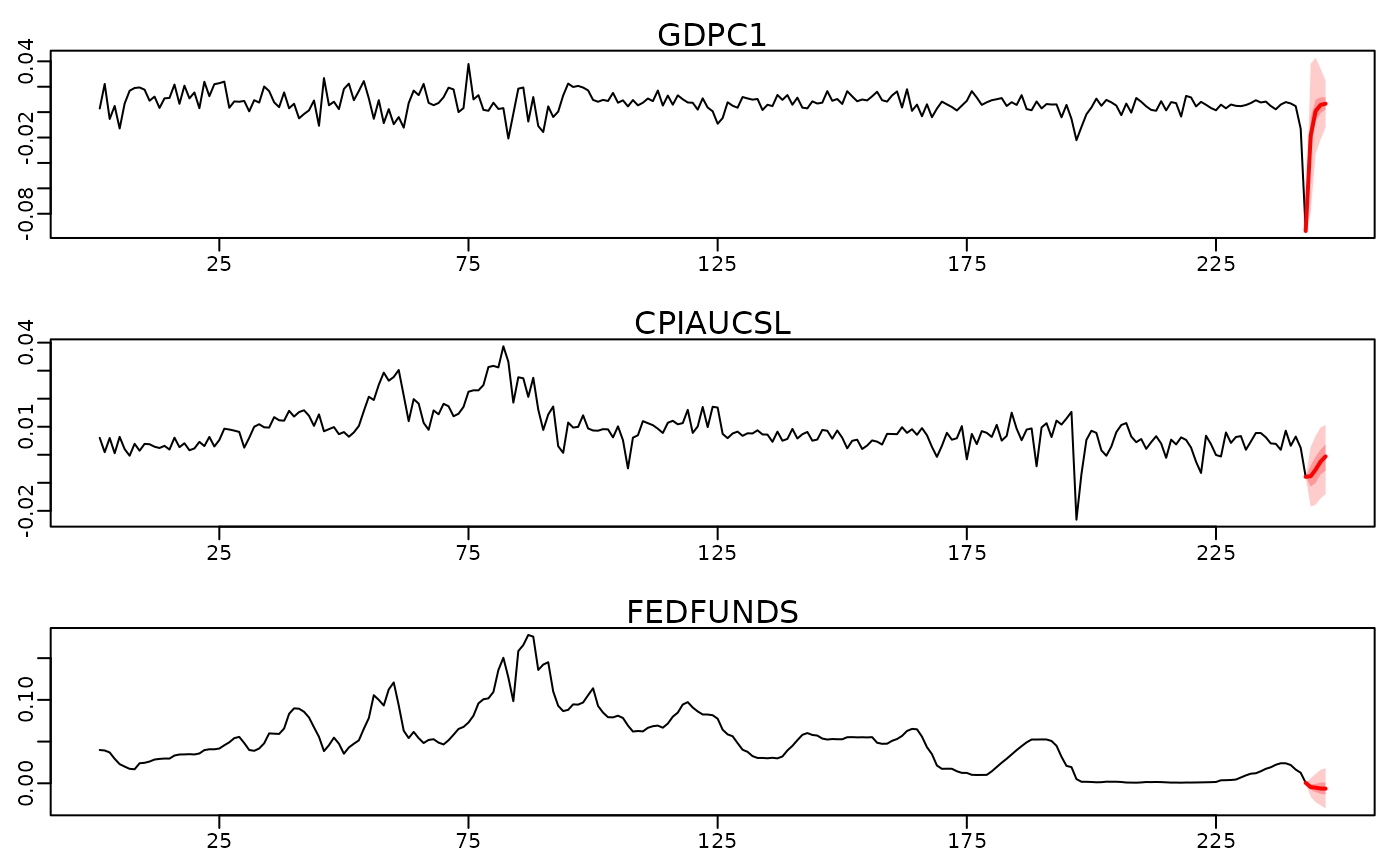# \donttest{
# In order to evaluate the joint predictive density of a subset of the
# variables (variables of interest), consider specifying 'LPL_VoI':
predictions <- predict(mod, ahead = 1:4, LPL = TRUE, Y_obs = test, LPL_VoI = c("GDPC1","FEDFUNDS"))
#> 'stable=TRUE': Calling 'stable_bvar()' to discard those posterior
#>           draws that do not fulfill the stable criterion.
#> 
#> 490/1000 stable posterior draws remaining for prediction!
predictions$LPL_VoI
#>      t+1      t+2      t+3      t+4 
#> 2.405161 6.277865 6.228728 6.194043 
# }